数据结构算法拾遗

目录

1 链表

1.1 LRU缓存

  • 配合哈希表实现

1.2 带头链表

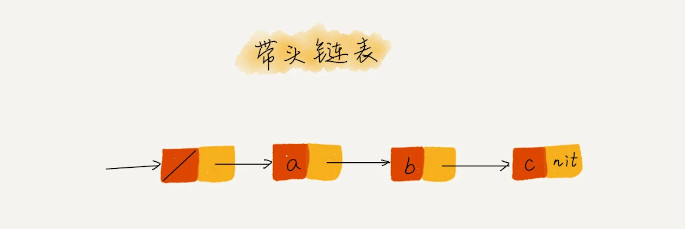
headedlist.jpg

  • 利用哨兵节点(无数据的头节点)

1.3 链表代码技巧

  1. 理解指针和引用的含义
  2. 警惕指针丢失和内存泄漏
  3. 利用哨兵简化实现难度
  4. 重点留意边界条件处理
    • 如果链表为空时，代码是否能正常工作？
    • 如果链表只包含一个结点时，代码是否能正常工作？
    • 如果链表只包含两个结点时，代码是否能正常工作？
    • 代码逻辑在处理头结点和尾结点的时候，是否能正常工作？

  5. 举例画图，辅助思考（ 举例法 和 画图法 ）

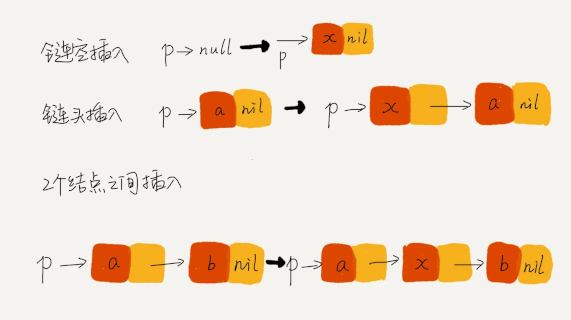
    linkedlist_hint.png

2 排序算法

2.1 评价标准

  • 执行效率
    • 最好情况、最坏情况、平均情况时间复杂度
    • 时间复杂度的系数、常数、低阶（数据规模不大时）
    • 比较次数和交换（或移动）次数
  • 内存消耗
    • 原地排序算法 O(1)
    • or 需要占用额外空间
  • 稳定性

2.2 冒泡排序

buble.png

  • 冒泡排序包含两个操作原子： 比较 和 交换
  • 优化：当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。
  • 最好时间复杂度：O(n) 数据已保持有序时

  • 平均复杂度：n个元素有n!种排列方式 概率推导很复杂。引入 有序度 概念

    • 有序度 是数组中具有有序关系的元素对的个数
    [1, 4, 3, 2, 5]
(1,4) (1,3) (1,2) (1,5) (4,5) (3,5) (2,5)
有序度为7
    • 满有序度 \(\frac{n(n-1)}{2}\) 5个元素为10

2.3 插入排序

insertion.png

  • 插入排序包含两个操作： 比较 和 移动
  • 移动操作的次数总是固定的，就等于逆序度。
    • 逆序度 = 满有序度 - 有序度
  • 平均复杂度 = 元素数 * 插入数组操作的平均复杂度(O(n)) = \(O(n^2)\)

2.4 选择排序

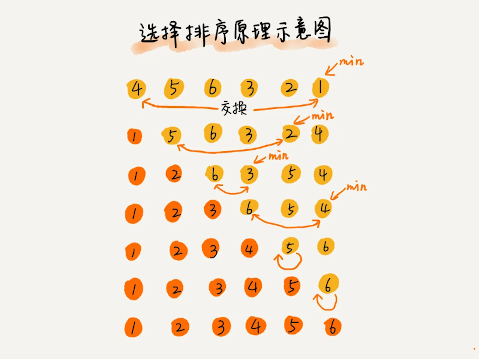
selection.png

  • 类似插入排序。选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。
  • 最好、最坏、平均复杂度均为 \(O(n^2)\)
  • 非稳定的排序算法