程序员的数学
1 数字0
如何定义\(10^0\)
不要死记其等于1。按规律来,\(10^3, 10^2, 10^1, 10^0\) ,每一个之间差了10倍,所以\(10^0=1\) 。\(10^{-1}\) 的结果同理。
- 这不是 记忆力 的问题,而是 想象力 的问题。目的是 简化规则 。
- \(0!=1\) 同理,简化递归规则 \(n!=n\times (n-1)!\) 即 \(1!=1\times 0!\)
0的作用:占位
用在按位计数法中,表示“没有”
- 现实中经典案例:通过没有药效的药,填满每日的服药例程中;简化了服药规则,病人只需要每天按时吃药就行,无需记服药日期。
历史
- 古埃及人:5进制和10进制混合计数,非按位计数法,不存在0
- 巴比伦人:仅两种符号表示1和10,硬件条件限制(粘土板),容易刻画。采用10进制和60进制,1小时60分钟即来源于此
- 玛雅人:从0开始数数,20进制
- 罗马人:罗马表示法,5为一个单元
- 印度人:十进制含0,现代计数源头;叫阿拉伯数字,是因为是阿拉伯学者将数字传入西欧。
2 逻辑
命题(proposition)的定义
能够判断对错的陈述句 叫做命题。同时满足true和false的不能称为命题,既不为true也不为false的也不能称为命题。
完整性及排他性
应用检查if语句逻辑
- 数值类型通过在数轴上画清边界值,通过查看有无“重复”或“遗漏”,分别判断排他性或完整性。
- 没有“遗漏”,具备完整性
- 没有“重复”,具备排他性
图表表示
- 真值表
- 文氏图
- 使用卡诺图简化逻辑
undefined
None and TrueisNone
3 计数
集合数量
- \(|A|\) 表示集合A的数量
排列
使用类似条件概率属性图的方式可帮助理解
组合
先排列后去重,分母中的 \(k!\) 即为去重操作
4 递归
通过递推公式求递归解析式全靠猜,需要数感和想象力
找出递归结构
- 从整体问题中隐去部分问题
- 判断剩余部分是否和整体问题是同一类问题
分布式归并排序
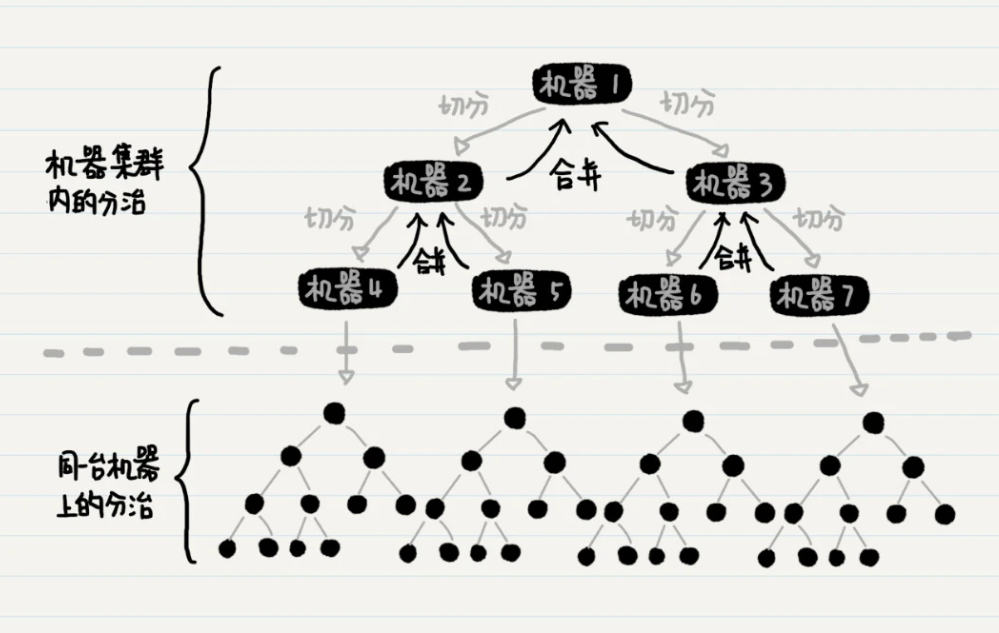 注意点:
注意点:
- 机器1、2、3都没有被分配排序的工作,只是在子结点的排序完成后进行有序数组的合并
- 另一种可能的数据切分方式是,每台机器拿出一半的数据给另一台机器处理,而自己来完成剩下一半的数据。
MapReduce架构

- 数据分割是指将数据源进行切分,并将分片发送到 Mapper 上。
- 映射是指 Mapper 根据应用的需求,将内容按照 键 - 值 的匹配,存储到哈希结构中。
- 归约是指接受到的一组键值配对,如果是键内容相同的配对,就将它们的值归并。
注意点:
- MapReduce 采用了哈希映射来分配数据,而普通的分治或递归不一定需要。
- 由于哈希映射的关系,MapReduce 还需要洗牌的步骤,也就是将键 - 值的配对不断地发给对应的 Reducer 进行归约。
- 在数据映射和洗牌之间,加入合并的过程,在每个 Mapper 节点上先进行一次 本地的归约 。
5 指数爆炸
对数
对数是解决指数爆炸的有效手段
- 对数的作用之一是可以将乘法运算变为加减法,指数爆炸情况下更容易发现规律
- 对数坐标轴:想象两个点同时乘以1.05倍,这1.05倍在坐标轴上的长度是一样的
涉及指数爆炸的四种处理方法
- 穷举拼性能
- 投机取巧,只需满足问题,变相求解;如哥尼斯堡七桥问题和铺设草席问题
- 求近似解:看需求,实用性强
- 概率求解:随机撞大运
6 解题思路
- 缩小问题规模(建议数字3和5)